Implementing The Sieve Of Eratosthenes in JavaScript

As a way of keeping my math skills sharp, I’ve recently started to work through the Project Euler set of computational math problems. They ask you not to post your work publicly, so I won’t be posting about any of my specific solutions, but I did think it would be fun to share about a helper method I’ve been using.

For several of the Project Euler problems I’ve worked on, I needed to be able to generate a list of prime numbers. To do that, I borrowed a Python implementation of the Sieve Of Erathosthenes from this StackOverflow answer. Since I haven’t had much reason to use generators in JavaScript yet, I thought it would be fun to translate that algorithm to JavaScript and share that here.

Sieve of Eratosthenes

The Sieve of Erathosthenes is a very old[1] simple algorithm for identifying prime numbers. In its normal implementation it is a useful way of finding small primes up to a certain number. Beginning at 2, the algorithm iterates upward. For the current number, if the number has not been marked, we identify it as a prime, and then mark all multiples of that number up to our target number. So to find all primes up to 12, we would

• start at 2, note 2 as prime, and mark 4, 6, 8, 10 and 12 as non-prime
• move to 3, note 3 as prime, and mark 6, 9, 12 as non-prime
• move to 4, see that it is marked, and skip it
• move to 5, note 5 as prime and mark 10 as non-prime
• move to 6, see that it is marked and skip it
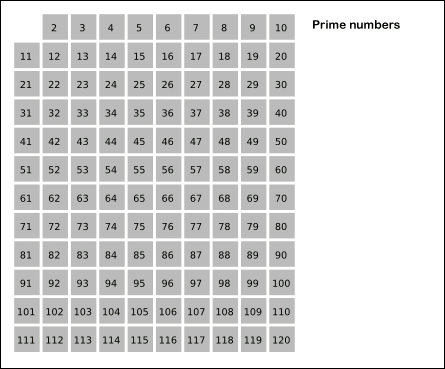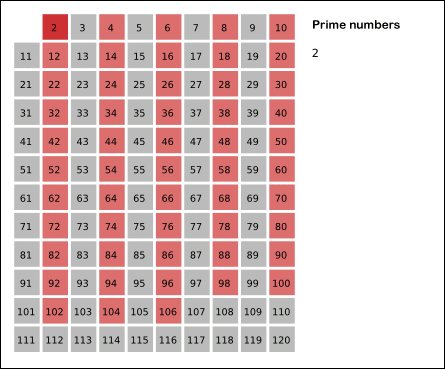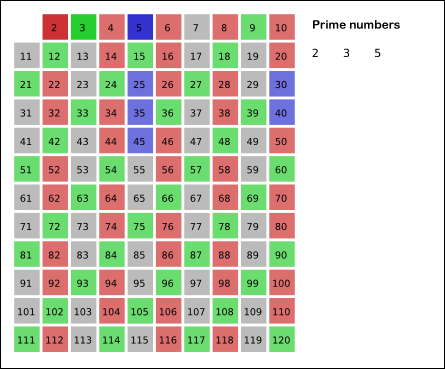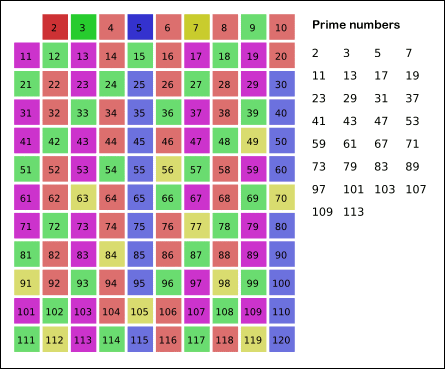
• move to 7 , note 7 as prime
• see that 8–10 are marked and skip them
• move to 11, note 11 as prime
• move to 12, see that it is marked and skip it

You can see it graphically with this visualization from Wikipedia:

Python Implementation

The Python implementation that I used makes some modifications to the classic version of the algorithm that lets it generate an indefinite number of primes while being memory efficient

def gen_primes():
    """ Generate an infinite sequence of prime numbers."""
    marked_not_prime = {}
    value_to_check = 2
    while True:
        if value_to_check not in marked_not_prime:
            yield value_to_check
            marked_not_prime[value_to_check * value_to_check] = [value_to_check]
        else:
            for prime in marked_not_prime[value_to_check]:
                marked_not_prime.setdefault(prime + value_to_check, []).append(prime)
            del marked_not_prime[value_to_check]
        value_to_check += 1

This version of the algorithm keeps a running set of the relevant matches, and keeps only the ones it needs. We can translate it more or less directly to JavaScript like this:

function* generatePrimes() {
    const markedNotPrime = {};
    let valueToCheck = 2;
    while(true) {
        if (!(valueToCheck in markedNotPrime)) {
            yield valueToCheck
            markedNotPrime[valueToCheck**2] = [valueToCheck]
        } else {
            let primes =markedNotPrime[valueToCheck];
            primes.forEach(prime=> {
                let nextMultipleOfPrime = prime + valueToCheck;
                if (nextMultipleOfPrime in markedNotPrime) {
                    markedNotPrime[nextMultipleOfPrime].push(prime);
                } else {
                    markedNotPrime[nextMultipleOfPrime] = [prime];
                }
            })
            delete markedNotPrime[valueToCheck];
        }
        valueToCheck += 1
    }
}

Let’s break down what this is doing.

function* generatePrimes() {
  //...
}

generatePrimes is a JavaScript generator. Generators “generate” a series of values in a “just in time” fashion; they only calculate the next value when it is needed, making them an efficient solution for working with large or infinite series. You specify a generator function by adding the * to the function declaration. Generators then use the yield keyword rather than return to return their values, and can yield multiple times. After a generator yields, it pauses execution until it is asked for another value. For our generatePrimes function, we are operating inside an infinite loop and will yield continuously without stopping[2].

const markedNotPrime = {};
let valueToCheck = 2;
while(true) {
    //...
    valueToCheck += 1
}

We’re using a plain object to keep track of our marked numbers, and using valueToCheck to keep track of where we are in iterating through numbers. As noted, we will iterate it forever if the generator continues to be called.

if (!(valueToCheck in markedNotPrime)) {
    yield valueToCheck
    markedNotPrime[valueToCheck**2] = [valueToCheck]
} else {
  //...
}

As in the original algorithm, if we get to a number that isn’t marked, we know that it is a prime. So we yield it, which pauses execution. If the generator is queried again, when we resume execution we mark the prime squared as not-prime, and we do that by assigning it an array with the current prime value in it. Using arrays for markers will make more sense in a moment. For now its worth noting that we only need to mark prime-squared as non-prime since every multiple below that is the current prime multiplied by a number less than it, which means it will already be covered, as we will see below.

if (!(valueToCheck in markedNotPrime)) {
  //...
} else {
    let primes = markedNotPrime[valueToCheck];
    primes.forEach(prime => {
        let nextMultipleOfPrime = prime + valueToCheck;
        if (nextMultipleOfPrime in markedNotPrime) {
            markedNotPrime[nextMultipleOfPrime].push(prime);
        } else {
            markedNotPrime[nextMultipleOfPrime] = [prime];
        }
    })
    delete markedNotPrime[valueToCheck];
}

Here’s the clever part of this implementation. When we hit a number that is marked as not-prime, instead of just skipping it and moving on, we use some logic to keep our list of marked values small and memory efficient. This is also what allows us to get an infinite list of primes instead of settling for those under a particular value. What we want to do is keep a list of all the primes that are factors of each marked number. Then when we hit a number that is marked, we mark the next multiple for each prime (valueToCheck + prime), and remove the current value from the object. That keeps checks fairly cheap by eliminating the number of marked numbers, and allows us to only add values to the marked list as we need them.

We can then use this code to get the 1,000,001st prime like this:

let gen = generatePrimes();
for(var i=0; i< 1000000; i ++) {
    gen.next()
}
console.log(gen.next().value)

That executed on my laptop in ~20seconds, approximately the same as the python implementation in python2, a little slower than running it under python3. I was curious whether using a Map for our marked prime list would speed things up:

function* generatePrimes() {
    const markedNotPrimeMap = new Map();
    let valueToCheck = 2;
    while(true) {
        if (!(markedNotPrimeMap.has(valueToCheck))) {
            yield valueToCheck
            markedNotPrimeMap.set(valueToCheck**2, [valueToCheck])
        } else {
            let primes =markedNotPrimeMap.get(valueToCheck)
            primes.forEach(prime=> {
                let nextMultipleOfPrime = prime + valueToCheck;
                if (markedNotPrimeMap.has(nextMultipleOfPrime)) {
                    markedNotPrimeMap.get(nextMultipleOfPrime).push(prime);
                } else {
                    markedNotPrimeMap.set(nextMultipleOfPrime, [prime]);
                }
            })
            markedNotPrimeMap.delete(valueToCheck);
        }
        valueToCheck += 1
    }
}

This version of the code runs about 25% faster, in 15 seconds on my machine. Not bad.

More Resources

• You can dig in more on the Sieve of Erosthenes on Wikipedia
• Check out Project Euler for some fun computational math problems.